Ever wondered why in some software geological 3D domains are converted to 2D sections and then re-constructed into a 3D volume? Or why a domain is described by its multiple triangulated boundaries instead of the domain as a volume itself? For us that did not seem logical. Therefore, in GEOREKA, a geological domain is a 3D volume and treated as such from beginning to the end. This little change in mindset has a great impact on the modelling process. Dealing with domains as volumes is a very intuitive approach and will quickly make you wonder why you ever did it differently.
THINKING IN VOLUMES
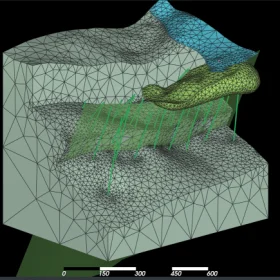
What does it mean for modelling? Do you need to re-learn how you modelled in the past? No, not at all. It means that every domain is represented by an implicit function such as an RBF. A complete geological model is then described by the relationships between these implicit functions. In turn, this model description is used to build a watertight output model.This approach allows you to choose the type of model for your output: a block model, triangulated solids, or a tetrahedral grid. GEOREKA is currently the only geological modelling software for the mining industry that can output tetrahedral girds, which can be used directly in geotechnical, geophysics, or flow modelling, or even modern geostats.
Note that triangulated solids are the boundaries of a tetrahedral grid and need to be converted to a tetrahedral grid for geotechnical, geophysics and other type of simulations.
General concept
As stated in the intro, any geological domain is a volume, not a boundary separating domains. Although this seems trivial, most modelling packages will force users to create boundaries between domains. Because of this, the whole concept in modelling geology changes. For volumetric modelling you do not define the actual boundary, but rather points that are inside the domain to model, and points outside of it.
This has small, but important consequences for modelling. No longer do you extract or digitize contact points, but convert intervals directly to indicator points representing either the inside and outside of a domain. Controlling the volume is done by manually adding inside, or outside points.
From domains to a geological model
Once a geological domain has been defined, the next step is to use it to create a model. In GEOREKA, this is done by specifying the relative age of the domain compared to other domains. A full geological model contains multiple domains represented by implicit functions. However, an implicit model does not know about other domains and will not ‘stop’ at the boundary of other domains and why we need to set the relationships between domains.
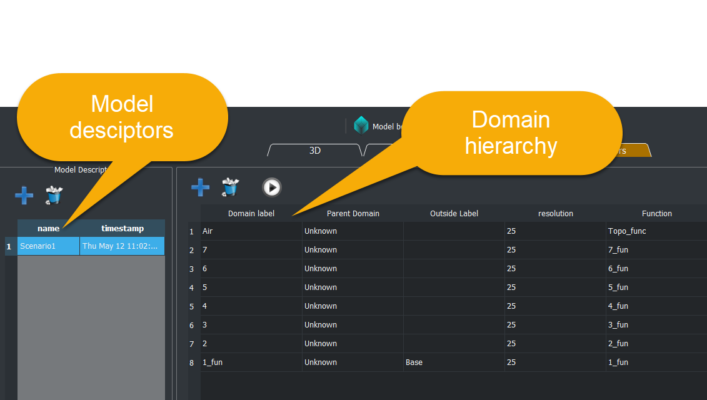
Our ‘Model Descriptor’ describes which domain is younger and therefore is used to define the final output volume of that domain. This means, that by default another domain cannot occupy that space.
Thinking in volumes becomes a logical way to build geological models. In addition, the model descriptor will act as a direct documentation of the interpreted geological age of the domains.
Tetrahedral models
Geological models in GEOREKA have always been created as tetrahedral meshes instead of blocks. With our newly added tetrahedral optimization step, these meshes now result in nicely distributed tetrahedra with fine resolution where required and coarse resolution elsewhere.
No more blocks?
One of the main reasons behind using tetrahedra is there improved accuracy. There is no need for sub-blocking, but also no need for partial estimates for blocks crossing a geological boundary. Tetrahedra adhere to boundaries exactly, meaning a tetrahedron is either inside a domain, or outside of it.
Moreover, due to the flexibility of their size and shape, tetrahedra can produce very sharp boundaries as shown in our examples. The base unit is a single volume with very sharp edges due to faulting, something nearly impossible to do with standard block models.
However, due to planning and other requirements, block models might still be needed. In that case, just switch the output of your model to be built and your model will consist of blocks.
No more triangles?
An advantage of tetrahedra over triangulated surfaces is that they are much less error prone. Triangles are 2D elements that have no volume by themselves. When a single triangle is missing in a model there is a hole and this can produce incorrect volume estimates. Tetrahedra are 3D elements and do have a volume. To get a volume estimate the volume of all tetrahedra are easily summed together. A ‘missing’ tetrahedron, if it would exist, would still result in a valid volume.
Secondly, to go from a triangulated solid to a block model, a costly blocking procedure is needed to do it correctly, or if the model is needed for flow simulation or geophysics a costly tetrahedral meshing step would be needed that converts the triangles and especially the internal volume into tetrahedra.
Since this is already included in all our models you get all the benefits: accurate volumes, efficient tetrahedral meshes suitable for further use in simulators.

